2015年陕西卷题
椭圆E:经过A(0,-1),且离心率为
求:(1)椭圆方程:
(2)经过点,且斜率为的直线与椭圆E交于不同的两点(均异于点A),证明直线AP与AQ的斜率之和为2.
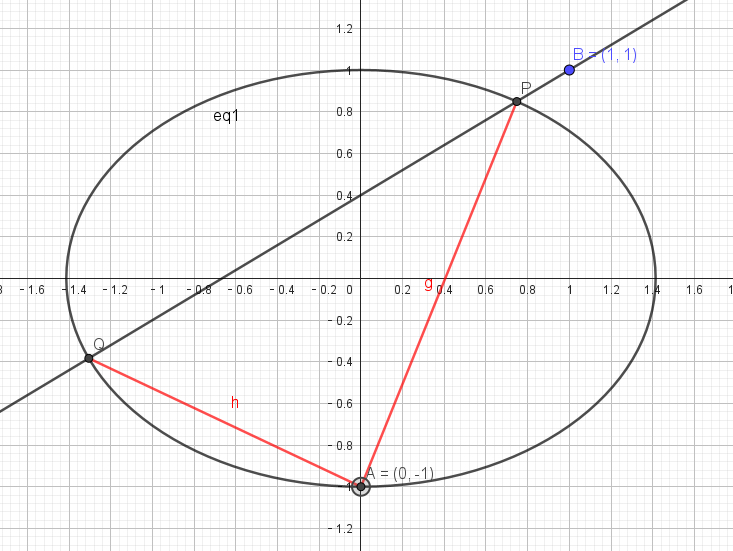
法一:
解:设过点(1,1)斜率为k的直线方程为:
PQ两点的坐标分别为,
题目显然要求我们证斜率之和=2
上式既含,未知数太多,设法消去,显然消去更容易,由于PQ两点在直线上,显然有,将其代入上式即可消去,而只含有
上式分子中前两项去括号合并同类项有:故有:
这时候出现我们最熟悉的,好了,我们要联立直线与椭圆的方程再利用韦达定理了。
上述仅是联立方程利用韦达定理,便能得到答案,方法简单容易理解,但是计算繁杂,只要认真耐心计算,便能得到正确的答案
法二:平移+齐次化。
上法分析可知,斜率为,,如果A在坐标原点,那么斜率和计算便容易得多!即为其实,这是很容易做到,我们只需要将点A(0,-1)向上平移一个单位即可。这样斜率计算就变得很简单了。当然,所有的元素(点、椭圆都要相应向上平移一个单位),平移并不影响直线斜率!
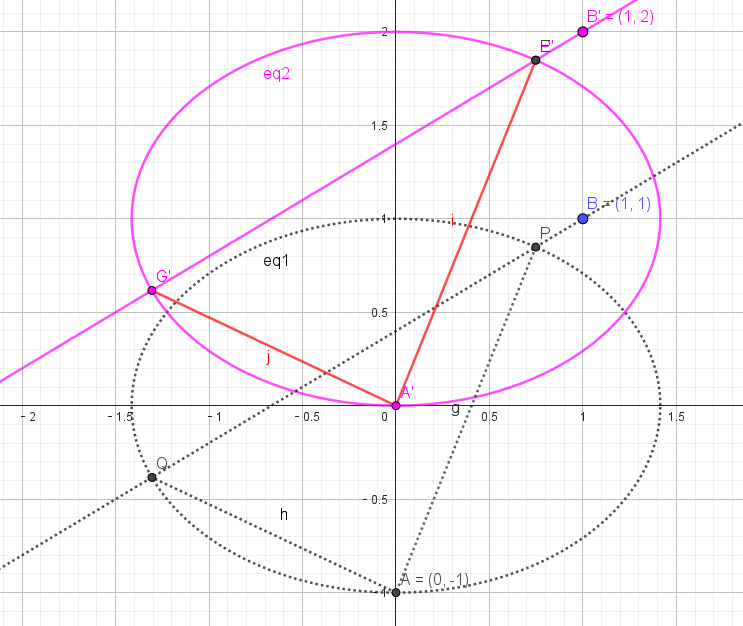
,
的本质上正向移=右移或上移为减,负向移=左移或下移为加。
故:A(0,-1)及(1,1)向上平移一个单位,变为A'(0,0)和(1,2),
椭圆E:向上平移一个单位得到
经过点的直线,我们要设成特殊的截距式,因为直线并不经过A的点,可以设成截距式
设过点的直线方程为:,这里是截距的倒数。直线设成这样,目的是进行齐次化!因为此时椭圆方程有一次项,如果一次项乘上1即变成二次项,式中每一项都变成二次项了。
此式左右两边除以,
千万别忘了,点(1,2)在直线上,即有
得证。
平移加齐次化解圆锥曲线问题,主要应用于过圆锥曲线的共点的两条直线斜率之和或积,将共点上下左右平移至原点,其余元素也作相应的平移。
下面分析一下,平移后的圆锥曲线方程乘上直线截距式方程的左边,齐次化后,得到有关的根就是直线与圆锥曲线的交点坐标。
回答这个问题前,让我们思考一下,为什么联立直线与圆锥曲线的方程,代入消元后,解得的就是直线与圆锥曲线的交点坐标?在思考这个问题之前,你大概只是记住了联立求解得到的结果就是交点坐标,怕是没有认真思考过为什么,即使思考过,也只是用数形结合,直线与圆锥曲线的交点,交点就是使得两者同时成立,联立的意思就是同时成立。嗯嗯嗯嗯嗯嗯嗯嗯,没错,但不全对。下面我肤浅分析一下方法一的联立方程:
我们把①式代入②,消去y,得到③式
,它的本质约束!
,它的意义就是满足受到x的约束条件,所代表的点在且仅在直线上。
它的意义也是满足约束条件,所代表的点在且仅在椭圆上。
将替换③中的③,此时③式中的既满足条件,也满足约束条件 ,也就是说,此时关于x的根是既在直线上,也在椭圆上,也就是两者的交点。
我们再来看一看方法二把A点向上平移一个单位后的椭圆的曲线方程:,它显然只是椭圆的约束方程。
再看看我们设的特殊的截距式直线方程:
它约束直线的条件是x,y满足而不是其余值时,所代表的点仅在直线。注意理解,这里是定值1,反过来说,也就是“1”不是随便的,必须满足受约束的。
而中令受到椭圆条件的约束,此时它的"1"是不受其它条件约束的。当我们将④中的“1”用⑥替换后,那么④式的就增加了约束条件了,即还要满足直线的约束。这个特殊的1,它等于mx+ny,它就是直线的约束条件。我们注入约束条件mx+ny的方法,是可以加1,减1,除以1,乘1,即便是乘1,也可以在任意地方乘的,但我们只在一次项的位置乘,目的是既能加上约束条件,又能完美齐次化。
我们再回头看,二元一次方程组的消元法,无论是代入消元,还是加减消元,其中的“加减”和“代入”的本质是注入约束条件,“消元”仅是求解方程和技巧和工具。换言之,我们也可以采用乘除注入约束条件的,只不过这样做你虽然可以注入约束条件,但你却没办法求出方程的根来,只有既能注入约束又能同时减少未知数的方法才能求方程的根。顺便提一下,我们高一利用“1”妙用,结合基本不等式求解最值的,其实乘以“1”的操作,也是注入约束条件。
至此,我们终于明白联立方程 这个符号的含义,就是注入约束条件,至于采用何种消元方法,则是解题技巧问题。因而,法二也可以采用联立直线与椭圆。即
当然,我们这样联立方程的目的并不是为了求解只含方程的根,我们的目的是为了求解含形如的根。这时候,我们必须采用的技巧出现了,它就是齐次化!说白了,这里齐次化与上面的消元都是解题技巧,只是目的不同,应用的技巧不同。
不知道,这样的表述是否有助于你们理解,齐次+平移法的逻辑原理。





